Localization with Trilateration Algorithm

 

Localization is a process by which a robot’s precise location and orientation is determined on a map.  The localization method must align with the electronics available for parameterizing the location algorithm.  We will be exploring the trilateration localization method, which calculates the robot’s location by measuring its distance from 3 known reference points called ‘anchors’.  This method is particularly useful when performing indoor localization with a known map.

 

The algorithm begins by measuring the robot’s distance from each of the anchors.  This example has known anchors at (1, 12), (7, 1), and (13, 12), and the green dot represents the robot’s current position.  In a real-world application, this data is not presented in a coordinate plane so the robot’s location cannot be so easily defined.  However, I will be using a coordinate plane in this example to explain how trilateration works for localization.  I’ve also written and published my own Trilateration Localization code to demo various anchor configurations!

 

 

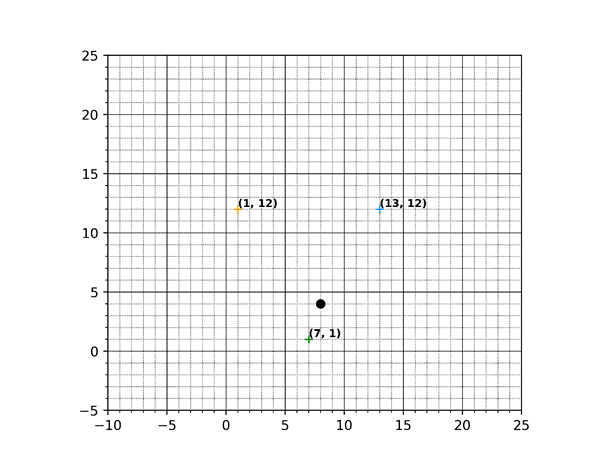
The robot is equipped with a tag, which communicates with each of the anchors to determine a distance measurement.  My application uses the DW3000 UWB modules for the anchors and the tag onboard the robot.  We know each anchor’s location and measure the distance between the tag and each anchor.  Since measurements don’t capture information about the robot’s direction or orientation, we assume the robot’s distance from all directions around each anchor – In other words, we draw a circle around each anchor using the tag’s measured distances as each circle’s radius to represent all potential robot positions.

 

Let’s work through the example!

 

Remember that a real-world implementation doesn’t operate on a clean coordinate plane.  Let’s assume that we don’t have a chart, and thus don’t know where the robot is located, but know where the anchors are located on a map and have successfully measured the tag-to-anchor distances.

 

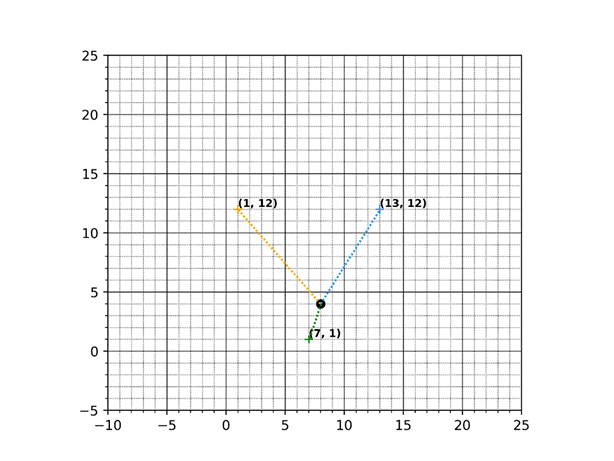
We begin a localization by measuring the distance between a tag and its known anchors and we do so with some measurement instrumentation.  We know that anchors are located at (1, 12), (7, 1), and (13, 12), and this demo clearly shows the robot’s position at (8, 4).  Since this is a localization exercise, let’s verify the robot’s position by stepping though the algorithm.

 

A real-world implementation will use instrumentation to measure the tag-to-anchor distances, but we will use a Euclidean distance calculation to yield the measurement.  Note that this calculation is NOT part of the algorithm – we are only using it to simulate the DW3000 UWB modules distance measurements.

 

·        Euclidean Distance: Measures straight-line distance between two points.  Allows diagonal movements.

 

 

We now have a collection of known values to parameterize the circles around each anchor.  Since anchors don’t move, their known positions, Anchor X Pos and Anchor Y Pos, are used as the center points around which each circle is drawn.  The distance between the robot tag and each known anchor is each circle’s radius.  These knowns can now be used to calculate the intersection of all 3 anchor circles.

 

Circle Parameter Definitions

 

 

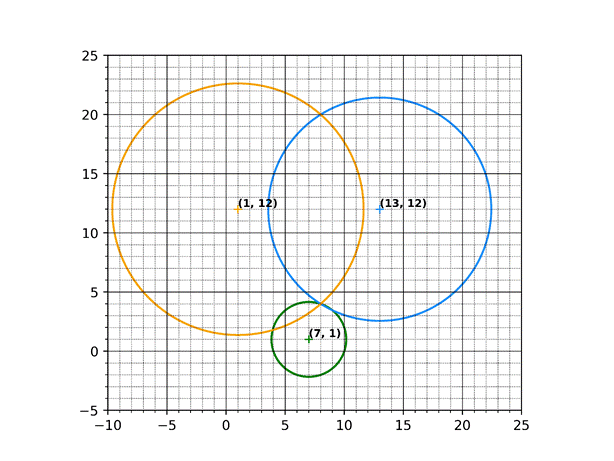
At this point we have 3 overlapping circles that have been fully parameterized, and we need to identify the point where all the circles overlap.  Since the circles are fully parameterized with known and measured information, we can solve a system of equations to find the unknown coordinates that all 3 anchor circles have in common. 

This common point is the point at which the circles intersect, defining the robot’s precise location!

 

 

Let’s do some calculations!

 

Before we begin, let’s define some variables that we’ll be using our localization calculations

 

Next let’s define the circles in their standard form.  We will represent these equations with variables that can be substituted with values from the Circle Parameter Definitions table above.

 

We can now expand each circle’s equation to isolate the unknown variable on one side and the known variables on the other. 

 

Now that each equation has been expanded, let’s isolate the unknown variables on one side of the equation and the known variables on the other. Doing so will allow us to calculate values for the unknown variables.

 

 

 

 

Let’s simplify:

 

 

We now have 2 equations and 2 unknowns, which allows us to solve a system of equations:

 

 

Helpful Resources

·        UWB Trilateration with ESP32, DW3000